The 'five number bet' holds the title for the worst bet in roulette. The house edge for this bet is 7.89%, and it's the only bet to have a bigger (worse) house edge than any other. Every other bet on a double-zero roulette has a house edge of 5.26%. Odds Of Winning – The ratio of wins to losses which gives you the odds. As an example, there are 37 numbers on a European roulette wheel and the straight up bet covers just one of those, so you can expect it to win one in every 37 spins, so the odds are 1 in 37.
All roulette bets chart.
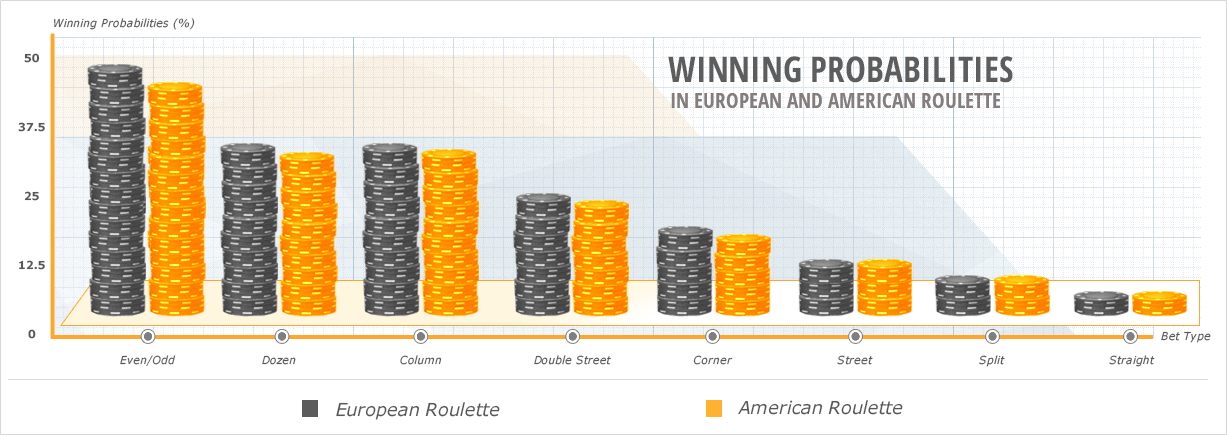
| Bet | Other Names | Payout | p European | p American |
|---|---|---|---|---|
| Red / Black | Colour bet | 1:1 | 48.65% | 47.37% |
| Even / Odd | 1:1 | 48.65% | 47.37% | |
| Low / High | 1-18 / 19-36 | 1:1 | 48.65% | 47.37% |
| Dozen | 2:1 | 32.43% | 31.58% | |
| Column | 2:1 | 32.43% | 31.58% | |
| 6 Number | Six line, Double street | 5:1 | 16.22% | 15.79% |
| 5 Number Bet* | Top line, Basket, First five | 6:1 | - | 13.16% |
| 4 Number | Corner, Square | 8:1 | 10.81% | 10.53% |
| 3 Number | Street, Line | 11:1 | 8.11% | 7.89% |
| 2 Number | Split | 17:1 | 5.41% | 5.26% |
| Single Number | Straight | 35:1 | 2.70% | 2.63% |
What Are The House Odds On Roulette
Key:
- Blue bets = outside bets. These are the bets that cover large, fixed sections of the table. These probability of winning with these bets is greater, but they have low payouts.
- Green bets = inside bets. These bets cover specific numbers on the table depending on where you place your chips. The payouts for inside bets are bigger, but the probability of hitting is lower.
* This bet can only be placed on a double-zero roulette table (i.e. on an American table and not a European or French one). It covers the numbers 0, 00, 1, 2 and 3.
Individual roulette bets in more detail.
Here is a quick overview on the different types of roulette bets and odds of each bet that can be made in roulette.
There is also a small image accompanying each bet to highlight how to place each of the bets at the table. Some of these bets you may well have previously overlooked, so pay attention!
The following list is ordered by the payout of each roulette bet, starting with the lowest payouts and moving to the bigger payouts as you scroll down. The payouts are in orange, and the win probability of each bet is in brackets in blue, assuming a European table (single-zero) is used.
Red / Black - 1:1(48.65%)
Also known as: Colour bet
| Payout | 1:1 |
|---|---|
| European Probability | 48.65% |
| American Probability | 47.37% |
| Total Numbers | 18 |
| Numbers Covered | Black = (2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35) Red = (1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36) |
A colour bet is a very popular bet, and gives odds of 1:1. So lets say for example you bet $5 on red, and after spinning the wheel the ball lands on red. You will get your $5 back, as well as an additional $5 in winnings, returning $10 in total.
Even / Odd - 1:1(48.65%)
| Payout | 1:1 |
|---|---|
| European Probability | 48.65% |
| American Probability | 47.37% |
| Total Numbers | 18 |
| Numbers Covered | Even = (2, 4, ..., 36) Odd = (1, 3, ..., 35) |
Similar to the colour bet, the even or odd boxes offer the same payouts with equal odds for hitting even or odd as there are for hitting red or black. Unfortunately, the green '0' does not count as either even or odd.
Low (1-18) / High (19-36) - 1:1(48.65%)
| Payout | 1:1 |
|---|---|
| European Probability | 48.65% |
| American Probability | 47.37% |
| Total Numbers | 18 |
| Numbers Covered | Low = (1 - 18) High = (19 - 36) |
These bets split the table in half, with one bet allowing you to bet on all of the lower half of the numbers (1-18) and the other half allowing you to bet on all of the higher numbers (19-36). Also known as the 'low bet' and 'high bet'.
Dozen - 2:1(32.43%)
| Payout | 2:1 |
|---|---|
| European Probability | 32.43% |
| American Probability | 31.58% |
| Total Numbers | 12 |
| Numbers Covered | 1st Dozen = (1 - 12) 2nd Dozen = (13 - 24) 3rd Dozen = (25 - 36) |
The dozen bet allows players to bet on 3 different sections containing 12 numbers, which are; 1-12, 13-27 and 28-36. This bet offers slightly higher odds (2:1) than an even money bet, but the chances of winning on one spin are a little lower.
Column - 2:1(32.43%)
| Payout | 2:1 |
|---|---|
| European Probability | 32.43% |
| American Probability | 31.58% |
| Total Numbers | 12 |
| Numbers Covered | 1st Column = (1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34) 2nd Column = (2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35) 3rd Column = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36) |
The column bet is very similar to the dozen bet, but instead splits the table into 3 sections length-ways rather than side-ways. Each of these bets also offer odds of 2:1, just as with the dozen bets.
What Are The Odds On Roulette Machine
6 Numbers - 5:1(16.22%)
Also known as: Six line bet, Double street bet
| Payout | 5:1 |
|---|---|
| European Probability | 16.22% |
| American Probability | 15.79% |
| Total Numbers | 6 |
| Numbers Covered | e.g. 10, 11, 12, 13, 14, 15 |
This particular bet is not always available at online casinos, but can still be played at the majority of them. Often overlooked by many novice players, this bet allows you to bet on 6 numbers at a time via a bet split between two adjacent rows.
Roulette Odds Table
5 Number - 6:1(13.16%)
Note: This bet can only be placed on American roulette tables (ones with the green 00).
Also known as: Five number bet, Top line bet, Basket bet
| Payout | 6:1 |
|---|---|
| European Probability | n/a |
| American Probability | 13.16% |
| Total Numbers | 5 |
| Numbers Covered | 0, 00, 1, 2, 3 |
The 'five number bet' holds the title for the worst bet in roulette. The house edge for this bet is 7.89%, and it's the only bet to have a bigger (worse) house edge than any other. Every other bet on a double-zero roulette has a house edge of 5.26%.
If you're playing American roulette – which you shouldn't be anyway – avoid this bet.
4 Numbers - 8:1(10.81%)
Also known as: Corner bet, Square bet
| Payout | 8:1 |
|---|---|
| European Probability | 10.81% |
| American Probability | 10.53% |
| Total Numbers | 4 |
| Numbers Covered | e.g. 11, 12, 14, 15 |
Also known as a 'square bet' or 'corner bet'. The 4 number bet allows you to bet on 4 adjoined numbers at a time. The chances of hitting any of these numbers is relatively low, but there is a decent payout for when you get lucky.
3 Numbers - 11:1(8.11%)
Also known as: Street bet, Line bet
| Payout | 11:1 |
|---|---|
| European Probability | 8.11% |
| American Probability | 7.89% |
| Total Numbers | 3 |
| Numbers Covered | e.g. 16, 17, 18 |
This bet involves similar placement to that of the 6 number bet, except for the chip is placed on the edge of one row, rather than spread across two. This bet is also known as the 'street bet' or 'stream bet'.
Alternative 3 number bets.
You can also place 3-number bets at the top of the table using the green zero(s). These can be placed in both single-zero and double-zero roulette, although you have an extra 3-number bet in double-zero roulette courtesy of that extra 00 number.
The payouts and probability for this bet are the same for the respective roulette tables as the street bet above.
2 Numbers - 17:1(5.41%)
Also known as: Split bet
| Payout | 17:1 |
|---|---|
| European Probability | 5.41% |
| American Probability | 5.26% |
| Total Numbers | 2 |
| Numbers Covered | e.g. 22, 23 |
This is where the odds start to get pretty big. A 2 number bet or 'split bet' allows you to bet on two adjacent numbers, offering you some pretty attractive odds of 17:1 - the second biggest payout available at a roulette table.
You can place a split bet across two numbers vertically or horizontally (if that makes any sense). In the screenshot above for example, you could just as easily bet on 22+25 or 22+19 instead of 22+23.
Single Number - 35:1(2.70%)
Also known as: Straight bet
| Payout | 35:1 |
|---|---|
| European Probability | 2.70% |
| American Probability | 2.63% |
| Total Numbers | 1 (no prizes, sorry) |
| Numbers Covered | e.g. 32 |
The single number bet or 'straight bet' is the big one, offering the greatest payouts at the roulette table of 35:1. Simply place your bet on one number and hope to get lucky.
Final thoughts.
So those are all of the different bets and odds of each of the bets when playing roulette online (or live for that matter). There is no restriction to how many different bets you can place at the roulette table, so go wild and see how it turns out. Just remember to enjoy yourself!
Read the article on 'called bets' for information on the special bets available on the racetrack roulette wheel. The snake bet is also worth a look if you're feeling fruity.

Probability
If one understands the basics of probability theory, then in roulette especially it is very easy to test betting systems mathematically. Here is the step by step logic of applying probability in roulette to the possible outcomes.
First, all the mathematics used here is based on a European single 0 wheel since the house edge is half the American version.
We know that the probability of an event happening is the chances of that event compared to all the possible events. For instance, when you flip a coin there are 2 possible outcomes: heads, tails. If you want to know what is the probability that the coin will come up heads, then that would be: heads / (heads + tails) = 1/2 = .5. Likewise when playing an even money bet at roulette, that option covers 18 of the 37 possible outcomes: 18/37=.48648649.
To find out the effect the odds have on a measurable outcome, we can apply that outcome to all possible results. So if we’re playing $1 on black, then we know that for 18 of 37 outcomes we will net $1 profit, and for 19 of the 37 possible outcomes we will net a $1 loss. ((18/37)*1)+((19/37)*-1)=-.02702703. This shows the house advantage on any single spin applied to your bankroll. We know that if you place $1 on any even number bet on average you will loose almost three cents per spin or $27 over 100 spins.
This is valuable when looking at more complicated betting within the layout of the table. For instance, if you consider on the thirds position that the return is 2:1. Let’s look at the extremes. If you place a bet on one of the three options, then you are obviously playing against probability: 12/37=.32432432 probability to win. If you place $1 on all three of the possible options, then for 36 of 37 numbers you will loose $2, make $2, and have the bet on the winning third returned to you for a net profit of $0. This of course makes no sense at all, but you’ll win almost every time if you’re in it to feel like a winner however if your considering a system you’re trying to make money. If we hedge the single bet with the second possible bet and place $1 on the first two of the thirds, then we cover 24 of 37 numbers 24/37=.64864865. We’re guaranteed to lose one bet, but if the other hits then we make $2, minus the one lost, plus the winning bet returned makes a net profit of $1 – and here’s the kicker – our chance of winning on any single bet is greater than 50% (64.86% to be precise).
We know that roulette is an independently random game where the results of one action does not affect the odds of a second action, so presented like this one might see this a winning system of finding a way to shift the odds in your favor. However if we analyze all the possible outcomes we see that the proposition is a losing one. 24 of 37 possible outcomes net us $1. On 13 of 37 possible outcomes we loose $2. So we plug in our formula: ((24/37)*1)+((13/37)*-2)=-.05405405. This is even worse than playing even money odds.
Now we come full circle. Almost all systems are based on the premise that the likelihood of an event happening repeatedly gets exponentially smaller the more times in a row one seeks that option. Probability will never rule out a roulette table showing the number 36 100 times in a row, but it will tell us exactly how unlikely it is. The premise is that the probability of an event happening once is multiplied by the likelihood of the second event multiplied by the third event and so on. For instance, for a single number to come up 100 times we multiply (1/37)*(1/37)*(1/37)… for one hundred times. This is a tiny number but we can see how fast it adds up:
(1/37)=.02702703
(1/37)*(1/37)=.00073046
(1/37)*(1/37)*(1/37)=.00001974
(1/37)*(1/37)*(1/37)*(1/37)=.00000053
The likelihood of a number coming up four times in a row is only 0.000053%, but it happens. Just go to Global Player Casino and check out the roulette results for the year. But I digress, the strategies say if you chase a loss long enough it won’t lose any more, and systems like the Martingale set it up so that you realize a profit when that condition fails. However, it’s still a losing system because we can plug in our formula to this just as easily as we can plug it into a single event.
But first let’s examine what it is we’re looking at. If we’re analyzing a system there are only two options we’re interested in: win or loss. Let’s not get too complicated and assume that one loss will exit the system and return the player to the starting state such as the Martingale.
If the first spin loses then we go to a second spin, and if the second spin loses then we go to the third and so on. So we know that for however many levels we examine all the preceding spins will be losses. In other words, if 51.4% of spins will lose, then we are looking at 51.4% of 51.4% will lose twice in a row and 48.6% of 51.4% will win on the second round. Therefore, 51.4% of 51.4% of 51.4% will lose thrice, and 48.6% of 51.4% of 51.4% will win.
For a single level we know that the formula is the probability of a win times the net result and the probability of a loss times the net result.
(((18/37)*1)+((19/37)*-1))= -.02702703
To check the second level, the probability of a loss followed by the probability of a win times the net result is compared to two losses and the net result.
(((19/37)*(18/37))*1)+(((19/37)^2)*-2)= -.27757487
To extrapolate the third, fourth, and fifth level:
((((19/37)^2)*(18/37))*1)+(((19/37)^3)*-4)= -.4133615
((((19/37)^3)*(18/37))*1)+(((19/37)^4)*-8)= -.49040931
We can see no matter how far we go on the Martingale system it’s always more likely a losing proposition than a wining proposition, and the deeper one goes the more likely one is to lose a greater sum of money. Of course this isn’t a surprise since the odds are already against us.
More on other systems and hedge betting later.
Any system can be analyzed like this for any game. If the result is positive, the odds are in the player’s favor. If the result is negative you’re trusting Lady Luck. I haven’t found a formula that results in a positive number. Of course, if I had I'd be in a casino right now.
This is a well presented maths explanation of the odds against the player when betting at roulette.But it confuses probability with certainty.Probability Theory deals with uncertainty not certainty.Roulette, like all gambling, is a game of chance so , obviously, chance is involved. This does not mean that only chance is involved.If the roulette wheel is random then no one can predict with certainty that we will win or lose. That certainty belongs to astrology not maths. There is no reason why the wheel should not give the same number continuously for a hundred, a thousand or even a million spins if it is truly random; incidentally, unless we are going to live till eternity then 'The Long Run' is irrelevant in real time betting.The writer errs when dealing with betting the First and Second dozens together. Using the 1-18 bet we can lower the odds against us. Placing three chips on 1-18 and one chip on the six-line 19-24 benefits us should zero occur whereas betting the two dozens does not.To my mind, there is an all too casual attitude to discussing roulette and this is exemplified in this article.Also- but not here -there is usually a knee-jerk reaction to anyone who rejects the notion that you are certain to lose. Claims of certainty -to win or lose -are unjustifiable where uncertainty clearly reigns.Gambling is Gambling is Gambling .